能否有一个数据结构既能兼顾高效率的动态修改，又能高效率的静态查找呢？

这就是我们的接下来要聊的话题：半线性结构：树。

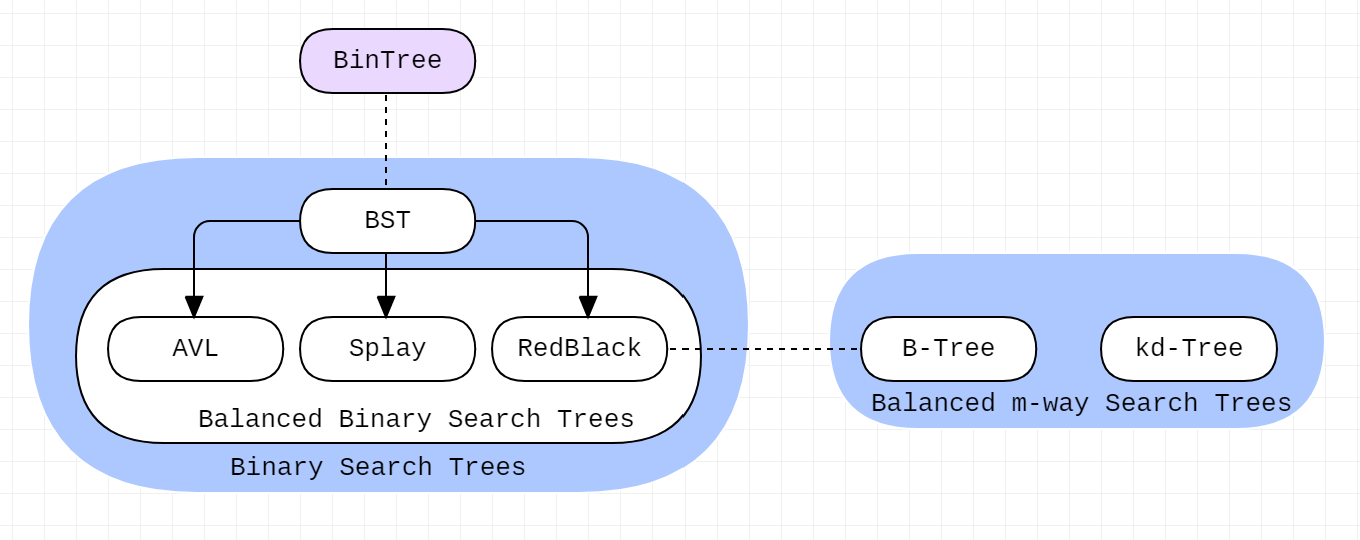
各数据结构特点：

数据结构	特点
BST(二叉搜索树)
AVL树
Splay(伸展树)	利用了局部性原理，保证刚访问过的元素再次访问时很快。且各操作均摊复杂度为$O(\log n)$
B-tree(B树)	由4阶B树演变而来，又称symmetric binary B-tree、half-balanced binary search tree
RB-tree(红黑树)
kd-tree(kd树)

各数据结构性能比较：（注意：比较时，我们不仅需要比较各个操作的时间复杂度，也要比较该数据结构所需的空间复杂度。）

数据结构	所需额外空间	search(搜索)	insert(插入)	remove(删除)
BST(二叉搜索树)		最快$O(1)$, 最慢$\Omega(n)$	最快$O(1)$, 最慢$\Omega(n)$	最快$O(1)$, 最慢$\Omega(n)$
AVL树	平衡因子、高度	$O(\log n) $	$O(\log n)$	$O(\log n)$
Splay(伸展树)		分摊$O(\log n)$	分摊$O(\log n)$	分摊$O(\log n)$
B-tree(B树)
RB-tree(红黑树)
kd-tree(kd树)

性能差异来源：

基本概念 #

为什么要引入这些概念？

call by key 和 call by index 和 call by order #

循秩访问(call by order)

循位置访问(call by position)

循关键码访问(call by key)

全序：全部元素之间可以相互比较，构成全序关系。例如：二叉树数据结构的key之间可以相互比较，我们维护全部key的全序关系，可以通过中序遍历得到单调非降的排序结果。

偏序：部分元素在全部元素的位置，构成偏序关系。例如：优先级队列，只需高效地跟踪全局的极值元素，其它元素一般无需直接访问。

二叉搜索树的性能主要取决于高度，故在节点数据固定的前提下，应尽可能的降低高度。当然，包含n个节点的二叉树，高度不可能小于$\lfloor log_2{n} \rfloor$

理想平衡：若树高恰好为 $\lfloor log_2{n} \rfloor$，则称作理想平衡树。例如：完全二叉树、满二叉树。

适度平衡：在渐进意义下适当放松标准之后的平衡性（例如：渐进地不超过$O(log{n})$），称作适度平衡。例如：AVL树、伸展树、红黑树、kd-树等。