translate from : https://en.wikipedia.org/wiki/Dominator_(graph_theory).
最近在学习SSA(Static Single Assignment)时, 遇到了${dominance frontier}$的概念, 所以google之, 简单翻译了一下wikipedia上对Dominator内容的介绍.
Dominator (graph theory) #
在计算机科学中, 在控制流图中, 如果从入口点到节点 $\bold{n}$ 的每条路径都经过节点 $\bold{d}$, 则称节点 $\bold{d}$ dominates 节点 $\bold{n}$
被写作 $\bold{d}$ dom $\bold{n}$ (or $\bold{d} \gg \bold {n}$).
另外我们定义, 每个节点都 dominates 它自身.
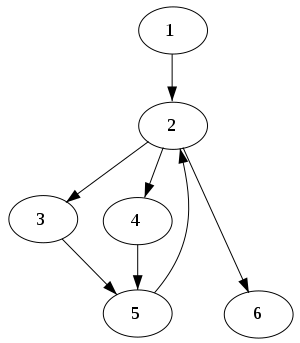
这里有一些相关的概念:
-
节点 $\bold{d}$ strictly dominates (严格支配) 节点 $\bold {n} $ : $\bold{d}$ dominates $\bold{n}$ 并且 $\bold{d} $ 与 $\bold{n}$ 不相等.
-
节点 $\bold{n}$ 的 immediate dominator (直接支配者) or idom : 一个节点严格支配 $\bold{n}$ 但是不严格支配其他严格支配$\bold{n}$ 的节点. 除了入口点之外, 每一个节点都有一个直接支配者.
-
节点 $\bold{d}$ 的 dominance frontier : 所有节点$\bold{n}$ 的集合, 使得 $\bold{d}$ 支配 $\bold{n}$ 的 immediate predecessor. 但是 $\bold{d} $ 不严格支配节点 $\bold{n}$ . 这是一组 $\bold{d’s}$ dominance 停止的节点集合.
-
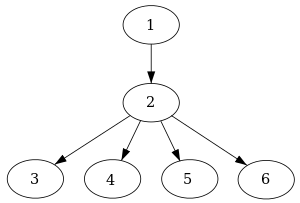
一个 dominator tree : 一颗树, 这棵树每个节点的子节点是它直接支配的节点. 因为直接支配者是独一无二的, 所以它是一棵树. 开始节点是树的根节点.
| 1 | $\color{black}{dom}$ | $\color{Gray}{1}$ | $\color{Red}{2}$ | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 2 | $\color{black}{dom}$ | $\color{Gray}{2}$ | $\color{Red}{3}$ | $\color{Red}{4}$ | 5 | $\color{Red}{6}$ | |
| 3 | $\color{black}{dom}$ | $\color{Gray}{3}$ | |||||
| 4 | $\color{black}{dom}$ | $\color{Gray}{4}$ | |||||
| 5 | $\color{black}{dom}$ | $\color{Gray}{5}$ | |||||
| 6 | $\color{black}{dom}$ | $\color{Gray}{6}$ |
| 与 domination关系相对应 |
|---|
| $灰色的节点\color{Gray}{灰色的节点}$ 是 非严格 dominated |
| $红色的节点\color{Red}{红色的节点}$ 是 直接 dominated |
dominator tree: