translate from: http://llvm.org/docs/tutorial/LangImpl02.html

介绍AST(抽象语法树)和Parser.
2.1 Introduction #
本章介绍如何使用Lexer, 来build一个完整的parser for our Kaleidoscope language. 一旦我们有了parser, 我们将会定义并且build 一个 AST.
2.2 AST #
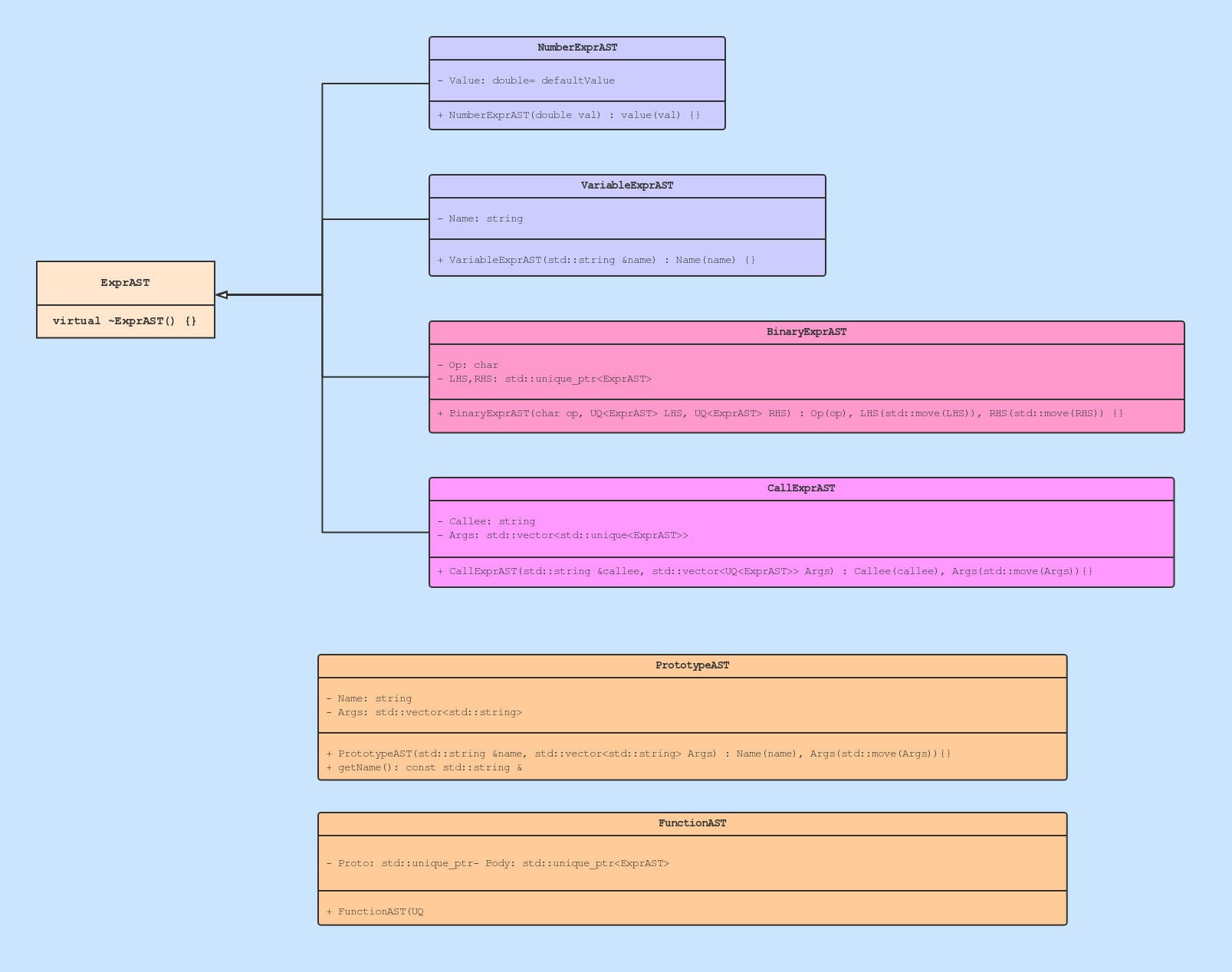
2.3 Parser Basic #
现在我们有了AST, 我们需要定义parser code来build it. 这里的想法是我们要解析类似于"x+y"(由词法分析器会返回3个Token)到AST中, 可以通过下面的代码产生:
auto LHS = llvm::make_unique<VariableExprAST>("x");
auto RHS = llvm::make_unique<VariableExprAST>("y");
auto Result = std::make_unique<BinaryExprAST>('+', std::move(LHS),
std::move(RHS));
Log
/// LogError* - These are little helper functions for error handling.
std::unique_ptr<ExprAST> LogError(const char *Str) {
fprintf(stderr, "LogError: %s\n", Str);
return nullptr;
}
std::unique_ptr<PrototypeAST> LogErrorP(const char *Str) {
LogError(Str);
return nullptr;
}
2.4 Basic Expression Parsing #
ParseNumberExpr:
/// numberexpr ::= number
static std::unique_ptr<ExprAST> ParseNumberExpr() {
auto Result = llvm::make_unique<NumberExprAST>(NumVal);
getNextToken(); // consume the number
return std::move(Result);
}
ParseParenExpr:
这里有一些有趣的点. 最主要的一点是 this routine eats all of the tokens that correspond to the production. 并且将next token返回到词法缓冲区中. (这不是一定要要求的), 这是一个实现递归下降parser的相当标准的写法.
a better example, 括号运算符的parser defined like this:
/// parenexpr ::= '(' expression ')'
static std::unique_ptr<ExprAST> ParseParenExpr() {
getNextToken(); // eat (.
auto V = ParseExpression();
if (!V)
return nullptr;
if (CurTok != ')')
return LogError("expected ')'");
getNextToken(); // eat ).
return V;
}
该函数说明了大量关于parser的有趣的事情:
-
展示了我们可以怎么样使用LogError. 当被调用的时候, 该函数期待current token是 ‘(’, 然后之后开始解析subexpression, (可能没有’)’ waiting), 如果用户输入"(4 x" 代替 “(4)”, the parser应该弹一个error. 因为error发生了, parser需要一种方法来表明error发生时, 程序会做什么.在我们的解析器中, 当error发生时, 我们会返回null.
-
另一个有趣的点是该函数使用了递归来调用ParserExpression(我们不久将会看到ParserExpression中调用了ParserParentExpr). 这是一种处理递归语法的相当不错的方法. 并且它保证每个过程都十分simple. 注意, 括号并不会引起AST node的构造. 当我们这样做的时候, 括号最重要的角色就是知道parser来提供grouping. 一旦parser成功构造了AST, 括号就不再被需要的.
下面的例子是处理变量引用和函数调用:
变量后面跟括号, 代表函数调用. 如果不是, 代码变量为identifier.
2.5 Binary Expression Parsing #
二元表达式很难解析, 因为它们通常是模棱两可的. 例如, 当给 the string “x+yz”, the parser可以选择"(x+y)z", 也可以选择"x+(yz)", 根据数学的定义, 我们的理解后面的是正确的. 因为 ““的优先级比”+“更高.
有很多种方法来处理它, 但是一种优雅的和有效的方法是Operator-Precedence-Parsing. 这种解析技术使用优先级来指导二元操作符递归处理. To start with, we need a table of precedences:
/// BinopPrecedence - This holds the precedence for each binary operator that is
/// defined.
static std::map<char, int> BinopPrecedence;
/// GetTokPrecedence - Get the precedence of the pending binary operator token.
static int GetTokPrecedence() {
if (!isascii(CurTok))
return -1;
// Make sure it's a declared binop.
int TokPrec = BinopPrecedence[CurTok];
if (TokPrec <= 0) return -1;
return TokPrec;
}
int main() {
// Install standard binary operators.
// 1 is lowest precedence.
BinopPrecedence['<'] = 10;
BinopPrecedence['+'] = 20;
BinopPrecedence['-'] = 20;
BinopPrecedence['*'] = 40; // highest.
...
}
对于Kaleidoscope基本的形式来说, 我们只支持4种二元操作符(很明显你可以扩展它, our brave and interpid reader). The GetTokPrecedence返回目前token的优先级, 如果不是二元操作符的话, 返回 -1. 通过一个map来增加一些操作符是一种不错的方法. 并且这很容易比较优先级.
有了上面的定义, 我们就可以解析二元操作符了. 运算符优先级解析的基本思想是:将具有可能不明确的二元运算符的表达式分成多个.
Ex: 表达式”a+b+(c+d)ef+g. operator precedence 将该表达式视为一个primary expressions流 separated by binary operators. 它将会先解析a, 然后[+, b] [+, (c+d)] [, e] [, f] and [+, g]. 注意括号也是primary expressions. 二元表达式不用担心它的subexpressions like (c+d) at all .
To start, an expression is a primary expression. 可能后面跟着[binop, primaryexpr].
/// expression
/// ::= primary binoprhs
///
static std::unique_ptr<ExprAST> ParseExpression() {
auto LHS = ParsePrimary();
if (!LHS)
return nullptr;
return ParseBinOpRHS(0, std::move(LHS));
}
ParseBinOpRHS是一个函数来解析一系列的pairs. 它需要一个优先级和指向表达式的指针.
注意 that “x” 是一个完全有效的表达式, 例如: “binoprhs” 可以是空的. 在这种情况下, it returns the expression that is passed into it. 在我们上面的例子中, 代码传递表达式"a"到ParseBinOpRHS 并且当前的token是 “+”;
传递给ParseBinOpRHS的优先级值表示函数被允许eat 的 the minimal operator precedence. 例如, 如果目前的pair stream is [+, x] and ParseBinOpRHS被传递的优先级是40, 它将不会消耗任何tokens(因为’+‘的优先级是20). 根据这种思想, ParseBinOpRHS starts with:
/// binoprhs
/// ::= ('+' primary)*
static std::unique_ptr<ExprAST> ParseBinOpRHS(int ExprPrec,
std::unique_ptr<ExprAST> LHS) {
// If this is a binop, find its precedence.
while (1) {
int TokPrec = GetTokPrecedence();
// If this is a binop that binds at least as tightly as the current binop,
// consume it, otherwise we are done.
if (TokPrec < ExprPrec)
return LHS;
该代码获得当前token的优先级, 并且检查它是否是too low. 因为我们定义无效的tokens的优先级是-1, 所以这隐式地可以知道(当run out of binary operators时, pair-stream就结束了).如果this check succeed, 我们知道token是一个二元表达式并且它将被included in this expression:
// Okay, we know this is a binop.
int BinOp = CurTok;
getNextToken(); // eat binop
// Parse the primary expression after the binary operator.
auto RHS = ParsePrimary();
if (!RHS)
return nullptr;
As such, this code eats(and remembers) 二元表达式 and 解析primary expression that follows. This build up the whole pair, the first of which is [+, b] for the running example.
现在我们解析表达式的左边和一组RHS sequence, 我们不得不决定which way the expression associates. 特别地, 我们 have “(a+b)” binop unparsed or “a+(b binop unparsed”. 为了确定这个, 我们look ahead at “binop” to 确定它的优先级并且将它与BinOp’s 优先级比较(which is ‘+’ in this case):
// If BinOp binds less tightly with RHS than the operator after RHS, let
// the pending operator take RHS as its LHS.
int NextPrec = GetTokPrecedence();
if (TokPrec < NextPrec) {
如果binop在"RHS"右侧的优先级低于或者等于我们当前运算符的优先级. in our example, 目前的操作符是”+" 并且下一个操作符是"+", 我们明白他们有相同的优先级. in this case 我们将会创建node for “a+b”, and then continue parsing:
... if body omitted ...
}
// Merge LHS/RHS.
LHS = llvm::make_unique<BinaryExprAST>(BinOp, std::move(LHS),
std::move(RHS));
} // loop around to the top of the while loop.
}
在我们的例子中. 这将把 “a + b” into “(a + b)“并且来执行下一次循环的迭代. with “+” as the current token. 上面的代码将被eat, remember, and parse (“c + d”) as the primary expression, which makes the 目前的pair equal to [+, (c + d)]. 它将会评估上面的"if"条件, 并将”“作为右侧的binop. 在该case中, 优先级 of “” 是比+的优先级更高, 因此if条件将会被输入.
关键的问题是: if条件如何解析右边的全部? In particular, 为了在我们的例子中正确的build AST. 它需要将”(c + d)ef"作为RHS表达式变量. 执行该操作的代码相当简单.
// If BinOp binds less tightly with RHS than the operator after RHS, let
// the pending operator take RHS as its LHS.
int NextPrec = GetTokPrecedence();
if (TokPrec < NextPrec) {
RHS = ParseBinOpRHS(TokPrec+1, std::move(RHS));
if (!RHS)
return nullptr;
}
// Merge LHS/RHS.
LHS = llvm::make_unique<BinaryExprAST>(BinOp, std::move(LHS),
std::move(RHS));
} // loop around to the top of the while loop.
}
在这一点上, 我们知道我们主要的RHS的二元运算符优于我们当前正在解析的binop. 因此, 我们知道任何运算符都优先于”+“的序列应该一起解析并作为"RHS"返回.
Example #
递归构造.
a+b*c*(d+e) + f:
第一次循环:
<!--1. [0, a] 和 [+, b]; [0, a] 为LHS; 0 < +, [1+, b] 继续ParseBinOpRHS-->
<!--2. [+, b] 和 [*, c]; [+, b] 为LHS; + < *, [*, c] 继续ParseBinOpRHS-->
<!--3. [*, c] 和 [(), d+e]; [*, c]为LHS -->
graph TB 1((a)) 2((b)) 3((c)) 4((d)) 5((e)) 7((+)) 8((*)) 9((*)) 10((+)) 7 --> 1 8 --> 2 8 --> 3 9 --> 8 9 --> 10 10 --> 4 10 --> 5 7 --> 9
第二次循环
graph TB 1((a)) 2((b)) 3((c)) 4((d)) 5((e)) 6((f)) 7((+)) 8((*)) 9((*)) 10((+)) 11((+)) 7 --> 1 8 --> 2 8 --> 3 9 --> 8 9 --> 10 10 --> 4 10 --> 5 7 --> 9 subgraph TB 11 --> 7 11 --> 6 end
2.6 Parse the Rest #
下一件事情是解析函数申明. in Kaleidoscope, extern函数申明以及函数体定义. 代码是相当直接的, not very interesting(once you’re survived expressions):
/// prototype
/// ::= id '(' id* ')'
static std::unique_ptr<PrototypeAST> ParsePrototype() {
if (CurTok != tok_identifier)
return LogErrorP("Expected function name in prototype");
std::string FnName = IdentifierStr;
getNextToken();
if (CurTok != '(')
return LogErrorP("Expected '(' in prototype");
// Read the list of argument names.
std::vector<std::string> ArgNames;
while (getNextToken() == tok_identifier)
ArgNames.push_back(IdentifierStr);
if (CurTok != ')')
return LogErrorP("Expected ')' in prototype");
// success.
getNextToken(); // eat ')'.
return llvm::make_unique<PrototypeAST>(FnName, std::move(ArgNames));
}
当然了, 函数定义是相当简单的, just 一个申明加一个表达式来实现函数体.
/// definition ::= 'def' prototype expression
static std::unique_ptr<FunctionAST> ParseDefinition() {
getNextToken(); // eat def.
auto Proto = ParsePrototype();
if (!Proto) return nullptr;
if (auto E = ParseExpression())
return llvm::make_unique<FunctionAST>(std::move(Proto), std::move(E));
return nullptr;
}
另外,我们支持extern来声明sin和cos之类的函数,以及支持用户函数的前向声明。这些extern只是没有身体的原型:
/// external ::= 'extern' prototype
static std::unique_ptr<PrototypeAST> ParseExtern() {
getNextToken(); // eat extern.
return ParsePrototype();
}
最后, 我们让用户输入任意顶级表达式并evaluate them. 我们将会处理this by defining anonymous nullary(zero argument) functions for them:
/// toplevelexpr ::= expression
static std::unique_ptr<FunctionAST> ParseTopLevelExpr() {
if (auto E = ParseExpression()) {
// Make an anonymous proto.
auto Proto = llvm::make_unique<PrototypeAST>("", std::vector<std::string>());
return llvm::make_unique<FunctionAST>(std::move(Proto), std::move(E));
}
return nullptr;
}
现在我们have all the pieces, let’s build a little driver that will let us actually execute this code we’ve built!
2.7 The Driver #
The Driver仅仅是通过调用所有的解析pieces.
/// top ::= definition | external | expression | ';'
static void MainLoop() {
while (1) {
fprintf(stderr, "ready> ");
switch (CurTok) {
case tok_eof:
return;
case ';': // ignore top-level semicolons.
getNextToken();
break;
case tok_def:
HandleDefinition();
break;
case tok_extern:
HandleExtern();
break;
default:
HandleTopLevelExpression();
break;
}
}
}
一件有趣的事情是: 我们忽略了顶级”;".
2.8 Conclusions #
通过这仅仅400行的代码, 我们定义了我们的最小的语言, 包含一个词法分析器, 解析器, 和AST builder.
这是一个简单的交互例子:
$ ./a.out
ready> def foo(x y) x+foo(y, 4.0);
Parsed a function definition.
ready> def foo(x y) x+y y;
Parsed a function definition.
Parsed a top-level expr
ready> def foo(x y) x+y );
Parsed a function definition.
Error: unknown token when expecting an expression
ready> extern sin(a);
ready> Parsed an extern
ready> ^D
$
2.9 Full Code Listing #
http://llvm.org/docs/tutorial/LangImpl02.html#the-abstract-syntax-tree-ast