translate from: https://en.wikipedia.org/wiki/Static_single_assignment_form
单一变量赋值
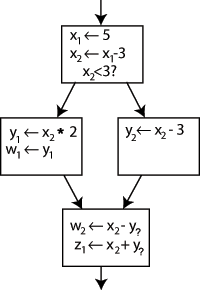
每个变量只被赋值一次.
在编译器设计中, static single assigment form (经常被称为SSA form 或者 简化为 SSA) 是IR的属性. 这要求每个变量只被assigment一次, 并且变量要在使用前定义. 原始IR中的已经存在的变量被划分为多个版本, 新的变量在文本中被显示为原始变量名称加下标的, 以便于每一个定义都有他们自己的版本.
Benefits #
SSA的主要用途: 来自于它通过简化变量的属性来同时简化和改进各种编译器优化的结果.
例如, 考虑这段代码:
y := 1
y := 2
x := y
我们可以一眼就看到第一行代码是不必要的, 第三行使用的y的值来自于第二行y的赋值. 一个程序必须执行 reaching definition analysis to 决定这个. 但是如果一个程序是SSA形式, 这些都是直接的:
y1 := 1
y2 := 2
x1 := y2
通过SSA的包含使用, 编译器优化 算法增强了很多:
- Constant propagation 常量传播
- Value range propagation
- Sparse conditional constant propagation
- Dead code elimination
- Global value numbering 全局值编号
- Partial redundancy elimination 部分冗余代码消除
- Strength reduction
- Register allocation
Converting to SSA #
将普通代码转换为SSA形式主要是通过使用新变量替换每个赋值的目标. and replacing each use of a variable with the “version” of the variable reaching that point.
例如, consider the following control flow graph:
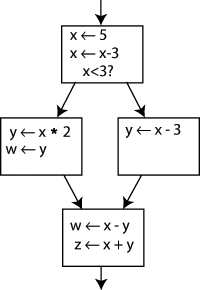
更改 “x -> x - 3” 左侧的名称, 并将之后对x的使用更改为新名称将使程序保持不变. 这可以通过在ssa中创建两个新的变量: x1 and x2 来利用, 每个变量只被分配一次. 同样, 给所有其他的变量也赋予不一样的下标.
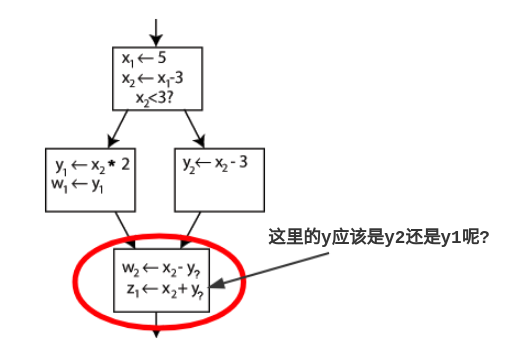
每一个使用都是很清楚的, 除了one case: 在底部block中,$\bold{y}$的使用应该是$\bold{y_1}$还是$\bold{y_2}$呢? 取决于控制流的path.
为了解决这个问题
在最后的块中插入了一个特殊语句$\bold{\phi(phi)} $ 函数. 这个表达式将会产生$\bold{y}$的新的定义, 通过选择$\bold{ y_1}$或者$\bold{y_2}$(取决于过去的控制流).
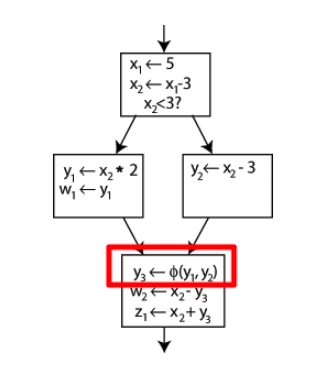
现在, 最后一个块可以轻松使用$\bold{y_3}$ , 并且可以获得正确的值. 一个$\bold{\phi}$ 函数 for $\bold{x}$ 是不必要的: 因为只有一个$\bold{x}$ 的版本. (换句话说: $\bold{\phi(x_2, x_2) = x_2}$ 是不必要的.
给定任意一个控制流图, 很难说出哪里需要插入 $\bold{\phi}$函数, and for which variables .
这个普遍的问题有一个有效的解决方案: dominance frontiers(支配边界) . (see below)
在大多数机器上: $\bold{\phi}$函数都没有被实现作为一个机器操作.
编译器只需在存储器(或者相同的寄存器)中即可轻松地实现$\bold{\phi}$ 函数. (存储器或寄存器作为一个$\bold{\phi}$函数输入的任何操作的目的地). 然而, 当simultaneous operations are speculatively producing inputs to a $\bold{\phi}$ 函数(就像很多机器上发生的那样), 该方法就不起作用了.
通常, 大多数机器都有一个选择指令被用于该情况中, 这可以被我们的编译器用于实现$\bold{\phi}$函数.
根据 Kenny Zadeck , $\bold{\phi}$ 函数最初被称为phony functions. 正式的名字是在学术paper上第一次发表时引入的.
computing minimal SSA using dominance frontiers(使用dominance边界计算最小的SSA) #
首先, 我们需要了解** dominator的概念: 如果不先经过节点 A 就到不了节点 B**, 我们就称节点 A 在控制流中严格支配节点 B. 这很有用, 因为如果我们已经到达节点 B , 就证明 A 中的代码也都正在工作. 如果 A 严格支配 B 或者 A = B, 我们就说 A dominates B ( 或者 B is dominated by A)
现在, 我们可以定义 the dominance frontier : 如果节点 A 不严格支配节点 B, 但是支配了一些 B的前面节点(predecessor), 就称为节点 B 在节点 A 的dominace frontier中. ( 可能节点 A 是 节点 B 的直接前节点. 然后, 因为任何节点都 dominates 它自身, 并且节点 A dominates 它自身, 所以节点 B 是处于节点 A的支配边界).
从 A 的角度看, 那是在其他控制路径上不经过A的 最早出现的节点.
Dominance frontiers 可以精准地确定我们需要$\bold{\phi}$ 函数的地方: 如果节点A定义了某个变量, then that definition and that definition alone (or redefinitions) will reach every node A dominates. 只有当我们离开这些节点并进入dominance frontiers 时,我们必须考虑其他流是否引入了相同变量的另外一个定义.此外, 控制流图中不需要处理其他 $\bold{\phi}$ 函数, 我们可以做到 no less.
一个算法可以用来计算dominance frontier set :
for each node b
dominance_frontier(b) := {}
for each node b
if the number of immediate predecessors of b ≥ 2
for each p in immediate predecessors of b
runner := p
while runner ≠ idom(b)
dominance_frontier(runner) := dominance_frontier(runner) ∪ { b }
runner := idom(runner)